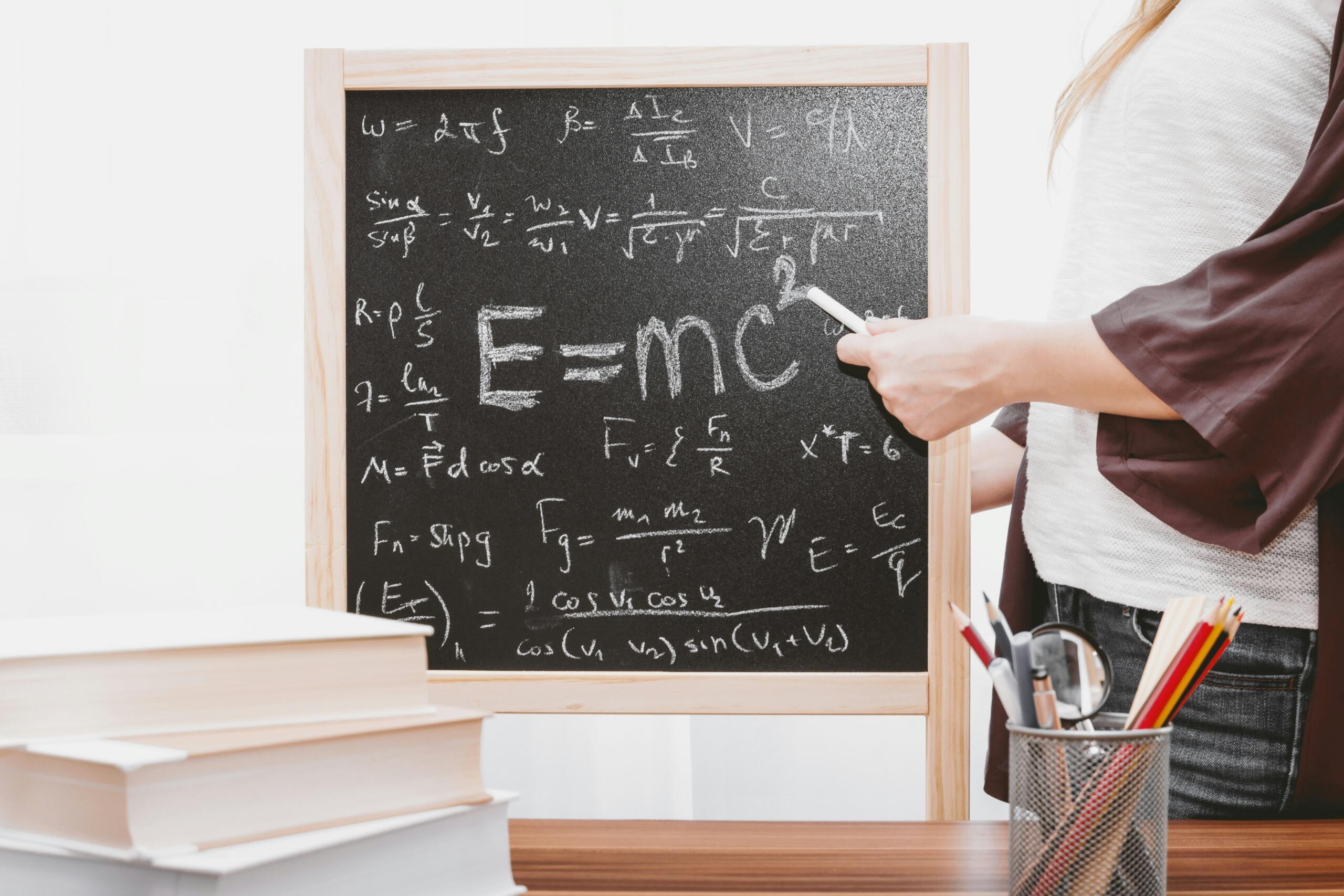Mida me teame, on ainult üks tilk, ja mida me ei tea, on terve ookean.
Isaac Newton
Matemaatika on universumi keel. Selle abil on sajandite jooksul avastatud ja selgitatud loodusseadusi, kujundatud tehnoloogiat ning mõtestatud maailma toimimist.
Matemaatika keskseks tuumikuks on valemid ja võrrandid. Need kuulsad võrrandid ja valemid on eksisteerinud ja püsinud aktuaalsed juba antiikajast kuni tänapäeva värskemate avastusteni. Iga uus matemaatiline võrrand ei anna mitte ainult vastuseid, vaid loob ka uusi küsimusi ning võimaldab meil jätkata teadmiste piiride nihutamist.
Siin on mõned matemaatilised võrrandid, mis on kujundanud meie arusaama maailmast ja selle toimimisest.

Pythagorase teoreem
Selle koolipingist ilmselt kõigile tuttava teoreemi juured ulatuvad aastasse 530 eKr. Julgeme väita, et tegemist on kõige tuntuima matemaatika võrrandiga.
Valem ise on järgmine:
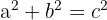
Pythagorase teoreem on moodsa matemaatika nurgakivi ning on andnud teadusharu arengusse määratlematu panuse. Isegi sajandeid hiljem on see kolmurkade kuninga valem meie mäludesse sügavalt talletunud.
Täisnurkse kolmnurga kaatetite (a ja b) ruutude summa on võrdne hüpotenuusi ruuduga (c).
Tänu Pythagorasele ja tema kuulsale teoreemile saame hõlpsasti arvutada täisnurksete kolmnurkade pikkuseid ja nurkasid ning määrata ruumilisi suhteid. Pythagorase teoreem on asendamatu vahend paljudes inseneri- ja teadusharudes. Selle abil on võimalik ehitada täpseid konstruktsioone ja teha keerulisi arvutusi.
Pythagorase teoreem on hea näide sellest, kuidas matemaatika on igapäevaelu lahutamatu osa, olenemata sellest, kas me teadvustame seda või ei.
Universaalne (Newtoni) gravitatsiooniseadus
17 . sajandil avastas Isaac Newton gravitatsiooniseaduse, mis väidab, et kõik kehad universumis tõmbuvad üksteise poole jõuga, mis sõltub nende massist ja nendevahelisest kaugusest.
See on üks tähtsamaid seaduseid, mis aitab seletada planeetide liikumist ja isegi väikeste objektide (näiteks õuna) kukkumist just maapinna suunas. See on aluseks paljudele teadus- ja kosmoseuuringutele.
Kaks keha tõmbuvad üksteise poole jõuga, mis on võrdeline nende kehade masside korrutisega ning pöördvõrdeline nendevahelise kauguse ruuduga.
Valem on järgnev:
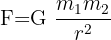
Kus:
- F on gravitatsioonijõud (N)
- m1 ja m2 on kehade massid (kg)
- r on kehade vaheline kaugus (m)
- G on gravitatsioonikonstant.
Newtoni gravitatsiooniseadus oli revolutsiooniline, sest see andis matemaatilise aluse Kepleri planeetide liikumise seadustele ja viis väljaõppeni ka Einsteinini relatiivsusteoorias.
Gravitatsiooniline vastastikmõju on universaalne ning mõjutab kõiki kehi. Teisest küljest, gravitatsioon avaldub ainult tõmbejõuna, st see ei põhjusta kehade vahel tõukumist.
Maa peal on gravitatsiooniline vastastikmõju võrreldes teiste samaaegselt rakenduvate vastastikmõjudega suhteliselt nõrk. Seevastu kosmoses on gravitatsiooniline vastastikmõju ainuke jõud, mis mõjutab kehade liikumist ning mängib planeetide ja galaktikate liikumises olulist rolli.
Relatiivsusteooria
Puhas matemaatika on omal moel loogiliste ideede luule.
Albert Einstein
Saksa teoreetilise füüsiku Albert Einsteini relatiivsusteooria muutis meie senist arusaama aegruumist ning tõi füüsikasse revolutsiooni. Teooria on jätkuvalt teaduslikes uurimistöödes fundamentaalse tähtsusega.
Selle tuntud teooria põhivalem on:
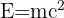
Siin:
- E tähistab energiat,
- m on mass,
- c on valguse kiirus vaakumis.
Lühidalt, see võrrand ütleb meile, et mass on energia vorm. Valguse kiirus vaakumis on väga suur arv, mistõttu isegi väike mass võib muunduda tohutuks energiaks. Seetõttu on valguse kiirus valemis ruudus, et näidata, kui tohutu hulk energiat võib peituda isegi väikeses massis.
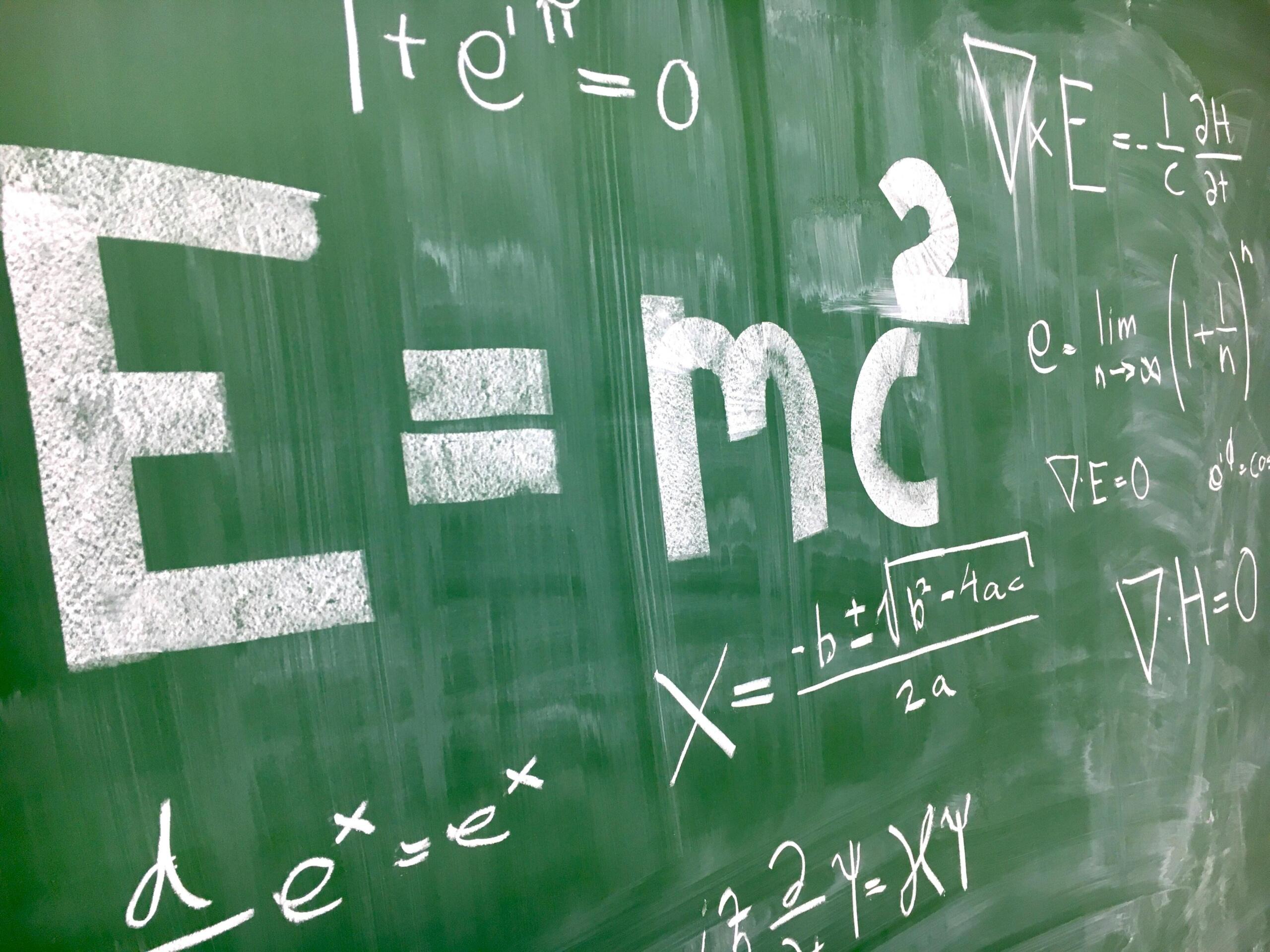
See valem, mis illustreerib nii erirelatiivsusteooriat kui ka üldrelatiivsusteooriat, muutis täielikult füüsikalist maailmapilti.
Valem püsib tänaseni äärmiselt oluline, sest see tõestab, et aine saab muunduda energiaks ja vastupidi 🤓
Relatiivsusteooria - mida Einstein ise nimetas invariantsusteooriaks - võttis kasutusele idee, et valguse kiirus on muutumatu universaalne konstant ja et aja kulgemine ei ole erinevate kiirustega liikuvate kehade puhul ühesugune.
Relatiivsusteooria on maailma üks kuulsamaid matemaatilisi teooriaid ning annab tõestust, kui oluline on matemaatikat õppida ja kuidas see ajaloo kulgu mõjutab. Sellel teoorial on olnud tohutu mõju tuumafüüsikas, astronoomias ja paljudes teistes teadusvaldkondades.
Ringjoone pindala
Ring on üks lihtsamaid geomeetrilisi tasapinnalisi kujundeid, mille kõik punktid on keskpunktist võrdsel kaugusel. Lihtsamalt öeldes on see suletud joon, mis meenutab sõrmust või rehvi.
Selle pindala arvutamise valem on järgmine:
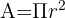
Kus:
- r on ringi raadius, st kaugus keskpunktist kuni ringi servani.
- A on ringjoone pindala
- π on matemaatiline konstant (3.1416...)

Ringjoone pindala arvutamine on oluline nii praktilistes olukordades – näiteks ümmarguse laua värvimisel – kui ka teaduses ja tehnikas.
Valemit kasutatakse laialdaselt inseneriteadustes, arhitektuuris ja disainis, olgu selleks siis sildade ehitamine, optikaseadmed või isegi kulinaarias pitsa õige läbimõõdu arvutamisel!
Tänu ringjoone pindala mõistele on võimalik paremini uurida lainefenomene, elektromagnetvälju, läätsede optilisi omadusi ning isegi valguse jaotumist ruumis.

Kaoseteooria
Kaoseteooria uurib ootamatut, mittelineaarset ja ettearvamatut – see on üks kuulsamaid matemaatikateooriaid.
See teooria käsitleb selliseid ettearvamatuid süsteeme ja nähtusi nagu turbulents, ilmastikunähtused, aktsiaturud, ajutegevus jpm. Neid nähtusi kirjeldatakse sageli fraktalite abil, mis omakorda illustreerib looduse lõpmatut keerukust.
Selle teooria kõige tuntum nähtus on nn „liblikaefekt“, mis tähendab, et väikesed muutused algtingimustes võivad viia tohutu erinevuse ja tagajärgedeni lõpptulemuses. Üks metafoore, mis seda efekti lühidalt kirjeldab (ning millest ka selle nimi on tuletatud), on see, et liblika tiivaplaksutus Brasiilias võib tekitada orkaani teisel pool maakera. Kõlab ulmeliselt, aga kaoseteooria kohaselt on see võimalik.
Meie igapäevaeludes leiab liblikaefekt pidevalt tõestust. Kuna meil ei ole kunagi piisavalt üksikasjalikku infot ühe kompleksse süsteemi kõikide algtingimuste kohta, ei suuda me ka selle lõpptulemust täpselt ennustada. See arusaam on aga otseses vastuolus näiteks arvamusega, et kasutades matemaatikat pokkerimängus kindlustame suurema tõenäosusega võidu – isegi imeväikesed vead süsteemi algtingimuste mõõtmisel võivad tohutult võimenduda, muutes igasuguse ennustamise tarbetuks. Huvitav, kas pole?
Kaoseteooria näitab, et matemaatika ei pruugi alati anda täpseid ja kindlasid vastuseid, vaid kirjeldab pigem tõenäosusi ning võimalusi.
Euleri identiteet
Matemaatikute arvates on Euleri identiteet (Euleri võrrand) üks elegantsemaid ja tähelepanuväärsemaid võrrandeid:
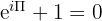
Selle erakordsus seisneb eelkõige selles, et võrrand seob omavahel mitmed fundamentaalsed matemaatilised konstandid üheainsas valemis:
- e (ehk Euleri arv) - naturaallogaritmi alus (2,71828...)
- i - imaginaararv (kus i2 = −1)
- π - irratsionaalne konstant pii (3.1416...)
- 1 ja 0: täisarvud
Euleri identiteet on võrrand, kus e on Euleri arv ehk naturaallogaritmi alus, i on imaginaararv, kusjuures i2 = −1, ning π on konstant pii ehk ringi ümbermõõdu ja läbimõõdu suhe.
💡 Euleri identiteedi võlu peitub tema lihtsuses ja universaalsuses.
Sellel on suur mõju inseneerias, arvuteoorias ja füüsikas. Euleri identiteet näitab hämmastavat seost eksponentsiaalsete, trigonomeetriliste ja imaginaararvude vahel, pakkudes sügavat sidet matemaatika eri harude vahel.
Termodünaamika teine seadus
Termodünaamika esimene seadus on sisuliselt energia jäävuse seadus, mis sätestab, et keha siseenergia muutub tänu väliskeskkonnast saadud soojusele ning tööle, mida süsteem välisjõudude vastu teeb.
Termodünaamika teine seadus toob mängu veel ühe suuruse, mida nimetatakse entroopiaks.
Tegemist on süsteemi korrastamatuse määraga, sest entroopia määrab, millistes suundades on energial võimalik potentsiaalselt muunduda.
Seetõttu on mõned looduslikud protsessid võimalikud samas kui mõned ei saa mitte kunagi toimuda. Seaduse selgitamiseks saab tuua lihtsa näite: kui me paneme jääkuubiku kuuma kohvi sisse, siis jääkuubik sulab ära, kuid kohv ei jäätu.
Termodünaamika teine seadus ütleb, et soojus liigub alati kõrgema temperatuuriga kehalt madalama temperatuuriga kehale, mitte vastupidi.
See füüsikaline seadus kehtestab piirangu soojusülekande suunale kehade vahel. Seadus põhineb eksperimentaalsete faktide üldistamisel ning on saanud hulgaliselt katselist kinnitust.
Kuigi selle seaduse põhimõtete väljatöötamisse on panustanud mitmed teadlased, siis laiema tuntuse saavutas see eelkõige 1873. aastal tänu Ludwig Boltzmannile ja Max Planckile. Seadus tutvustas entroopia mõistet, mis määrab, millises suunas energia muundumised toimuvad.
Kujutleme, et paneme jääkuubiku tassi kuuma teesse.
Mis juhtub?
Täpselt nii – jää hakkab sulama.
Termodünaamika teine seadus seletab, miks see juhtub, ja miks vastupidine – see, et jää külmutaks tee – ei ole võimalik.
Schrödingeri võrrand
See kvantmehaanika võrrand on samuti üks tuntumaid võrrandeid matemaatikas. Ei, me ei räägi seekord mitte Schrödingeri kassist, vaid tema ühest teistest geniaalsest ideest, mis pälvis ka Nobeli füüsikapreemia.
Schrödingeri võrrand kirjeldab osakeste käitumist ajas ja ruumis. See aitab kirjeldada erinevaid olekuid, milles osake võib eksisteerida.
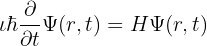
See võrrand selgitab, kuidas kvantosakesed liiguvad ja kuidas nende lainefunktsioonid ajas erinevad.
Lisaks tehnilisele tähtsusele tõstatab see võrrand ka intrigeeriva filosoofilise küsimuse: kas mateeria koosneb tõesti konkreetsetest füüsikalistest olekutest (tahke, vedel ja gaas), või on tegemist millegi enamaga? Teisisõnu, see kutsub meid üles mõtlema aine tõelise olemuse üle ning kuidas me seda tajume. Sellised matemaatilised mõistatused on tavalised ning Schrödingeri võrrand avab ukse vastustele, mis võivad tulevikus ilmsiks tulla.
Schrödingeri võrrand on olnud väga kasulik näiteks tuumaenergia arendamisel ja pooljuhtide uurimisel ning ka ka arvuti- ja lasertehnoloogia valdkondades.
Tänu sellele võrrandile sai võimalikuks aatomite ja subatomaarsete osakeste käitumise selgitamine.
Schrödingeri võrrand selgitab osakeste muutusi ajas. See kirjeldab osakese võimalikke olekuid, mille põhjal on omakorda võimalik kirjeldada mistahes füüsikalist süsteemi.
Maxwelli võrrandid
Maxwell neli võrrandit moodustavad elektromagnetismi aluse. Need võrrandid kirjeldavad elektri- ja magnetväljade vastastikmõju ning on olnud ülimalt olulised nii elektrodünaamika kui ka relatiivsusteooriale arengus.
Maxwelli võrrandid on järgmised:
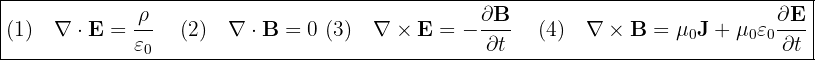
- (1) - Gaussi seadus elektrivälja jaoks
- (2) - Gaussi seadus magnetvälja jaoks
- (3) - Faraday elektromagnetilise induktsiooni seadus
- (4) - Ampère'i-Maxwelli seadus
Maxwelli võrrandite avastust peetakse klassikalise füüsika haripunktiks, sest neist saab tuletada kõik elektromagnetismi valemid. Võrrandid kirjeldavad elektri- ja magnetväljade vastastikmõju ning nende seost elektriväljade ja laengutega.
Nii elektri- kui ka magnetvälju saab kujutada väljavooludiagrammide abil. Maxwelli võrrandid on kindlasti mõjutanud matemaatika tähtsust tänapäeva maailmas, illustreerides taaskord, kuidas matemaatikal on meie eludes elementaarne roll.
Lihtsamalt öeldes on elektri- ja magnetväljad omavahel seotud. Nad mõjutavad üksteist ning neid saab muuta ja modifitseerida.
Tänu Maxwelli võrranditele on võimalik mõista raadiolaineid, valguse olemust ja selliseid kaasaegseid tehnoloogiaid nagu raadioside ja laserid.
Matemaatika universaalne keel
Kõik need kuulsad võrrandid on matemaatika arengule suuresti kaasa aidanud. Lisaks nende otsesele väärtusele kui teadmiste kogumid on nad võimaldanud luua ja täiustada ka teisi matemaatilisi kontseptsioone.
Kõiki loetletud matemaatilisi võrrandeid ühendab see, et nad on oma lihtsuses elegantsed, lühikesed ning aitavad ühendada matemaatika põhialused lihtsamate mõistetega. Kõigil neil võrranditel on ulatuslikud ja põhjalikud rakendused igapäevaelus ja erinevatel erialadel, mis omakorda lisab neile väärtust. Kuigi nendega seotud matemaatika võib olla mõnevõrra keeruline, on nad sellegipoolest põnevad ja kaasahaaravad.
Matemaatika keel on universaalne ning ei tunne keelebarjääre. Ei loe, kas räägid eesti, inglise, prantsuse või hispaania keelt. Kui sa mõistad matemaatikat, siis suudad sa end selles igas keeles arusaadavaks teha. Matemaatika on selleks, et me saaksime universumi avastada ja mõista selle toimimist, kasutades selleks ühist ja kõigile üheselt arusaadavat keelt - matemaatika keelt.
matemaatikaalast teadustööd
Kokkuvõte AI abil: